lambda演算系列搬运cgnail的blog，源blog连接为这里。

在前面的几个帖子里，我已经建立了如何把lambda演算变成一个有用的系统的点点滴滴。 我们已经有了数字，布尔值和选择运算符。我们唯一欠缺的是重复。

这个有点棘手。lambda演算使用递归实现循环（递归的解释可以看这里）。 但是，由于在lambda演算里函数没有名字，我们得采取一些非常手段。这就是所谓的Y组合子，又名lambda不动点运算符。

让我们先来看看lambda演算之外的一个简单的递归函数。阶乘函数，这是标准的例子：

1
2
factorial(n) = 1 if n = 0 
factorial(n) = n * factorial(n-1) if n > 0

如果我们要用lambda演算来写的话，我们需要几个工具……我们需要一个测试是否为零的函数，一个乘法函数，以及一个减1的函数。

为了检查是否为零，我们将使用一个命名函数IsZero，它有三个参数：一个数字，两个值。如果数字为0，则返回第一个值；如果它不为0，则返回第二个值。

对于乘法——我们在制定出递归之前写不出乘法。但我们可以假设目前有一个乘法函数 Mult x y。

最后，减1函数，我们用Pred x表示x的前驱——即x - 1。

所以——第一版的阶乘，如果我们把递归调用留做空白的话，将是：

1
lambda n . IsZero n 1 (Mult n ( something (Pred n)))

现在的问题是，我们怎么填上“something”，使其递归？

答案是一些所谓的组合子。一个组合子是一种特殊的高阶函数，它们只引用函数应用。（一个高阶函数是一个函数，它接受函数作为参数，并且返回的结果也是函数）。Y组合子非常特殊，它有近乎神奇的功能使得递归成为可能。它的样子如下：

1
let Y = lambda y . (lambda x . y (x x)) (lambda x . y (x x))

看了公式，你就就明白为什么叫它Y了，因为它的“形状”像一个Y。为了让这一点更清晰，有时我们把它写成树的形式。下面是Y组合子的树：

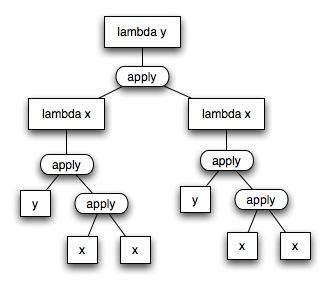
y-combinator

Y组合子的特别之处在于它应用自身来创造本身，也就是说 (Y Y) = Y (Y Y)。让我们从(Y Y)开始看看它如何工作：

  • Y Y
  • 展开第一个Y：(lambda y . (lambda x . y (x x)) (lambda x . y (x x))) Y
  • 现在，beta规约：(lambda x . Y (x x)) (lambda x . Y (x x))
  • alpha[x/z]变换第二个lambda：(lambda x . Y (x x)) (lambda z. Y (z z))
  • beta规约：Y ((lambda z. Y (z z)) (lambda z. Y (z z)))
  • 展开前面的Y，并alpha[y/a][x/b]变换：(lambda a . (lambda b . a (b b)) (lambda b . a (b b))) ((lambda z . Y (z z)) ( lambda z . Y (z z)))
  • beta规约：(lambda b . ((lambda z. Y (z z)) (lambda z. Y (z z))) (b b)) (lambda b . ((lambda * z. Y (z z)) (lambda z. Y (z z))) (b b))

现在，仔细看该表达式。这是(Y (Y Y)) [记得前面的(Y Y) = (lambda x . Y (x x)) (lambda x . Y (x x))吧]。所以， Y Y = Y (Y Y)，这是Y的魔力：它再造了本身。(Y Y) = Y (Y Y) = Y (Y (Y Y))，子子孙孙无穷匮也。

那么，我们如何使用这个疯狂的玩意？

好吧，让我们拿我们的第一次尝试做一下修改。给它取个名字，并尝试使用该名字重写：

1
let fact = lambda n . IsZero n 1 (Mult n (fact (Pred n)))

现在的问题是，“fact”不是“fact”中定义的标识符。我们如何让“fact”引用“fact”呢？好了，我们可以做一个lambda抽象，让“fact”函数作为参数传过去；于是，如果我们能找到一种方法来写“fact”，使得我们可以把它作为一个参数传给它自己，事情就搞定了。我们称之为metafact。

1
let metafact = lambda fact . (lambda n . IsZero n 1 (Mult n (fact (Pred n))))

现在，如果我们可以应用metafact到本身，我们就得到了我们的阶乘函数。也就是说，

1
2
3
4
5
6
7
8
9
fact n = (metafact metafact) n 。
        <= (lambda f1 . lambda t1 .  t1 ? 1 : t1 * f1 (P(t1))) (lambda f2 . lambda t2 .  t2 ? 1 : t2 * f2 (P(t2))) n  
        <= (lambda t1 .  t1 ? 1 : t1 * (lambda f2 . lambda t2 .  t2 ? 1 : t2 * f2 (P(t2))) (P(t1))) n
        <= lambda n .  n ? 1 : n * (lambda f2 . lambda t2 .  t2 ? 1 : t2 * f2 (P(t2))) (P(n))
        <= lambda n .  n ? 1 : n * (lambda f2 .  P(n) ? 1 : P(n) * f2 (P(P(n))) ) 
        <= lambda n .  n ? 1 : n * (lambda f .  (P(n) ? 1 : P(n) * f (P(P(n))) )
        <= lambda n . n ? 1 : n * (lambda f . f (P(n)))
        <= lambda f . lambda n . n ? 1 : n * f (P(n))
        <= f (n)

这正是Y的用武之地。它让我们可以创建一个古怪的结构，每次需要递归的时候都可以复制函数过来。metafact (Y metafact)将得到我们想要的。展开之，这就是：

1
(lambda fact . (lambda n . IsZero n 1 (Mult n (fact (Pred n))))) (Y (lambda fact . (lambda n . IsZero n 1 (Mult n (fact (Pred n))))))

(Y metafact)实际上是第一个lambda中参数fact的值；当我们对它做beta规约的时候，如果n为零，那么它只是返回1，如果它不为零，那么它调用fact (Pred n)。 然后再将factbeta规约为Y metafact， 这个变换疯狂地复制，得到输出metafact (Y metafact) (Pred n)。

瞧，递归（metafact (Y metafact) = metafact (Y metafact) (Pred n)）。极度扭曲的递归。

我第一次了解了Y组合子是在本科，1989左右，至今我仍然觉得它很神秘。我虽然也明白它是怎么来的，但我无法想象地球上怎么会有人把它给想出来！

如果你对此很长感兴趣，那么我极力推荐「The Little Schemer」这本书。这是本非常棒的小书 —— 写得象一本儿童读物。书里要么每一页正面是一个问题，背面就是答案，要么一页分成两栏，一栏问题一栏答案。书的风格轻松幽默，不仅教你Scheme编程，更教人怎么思考。

一个重要的提示：实际上有几个不同的版本的Y组合子。也有几种不同的lambda演算的计算方式：给定以下表达式：

1
(lambda x y . x * y) 3 ((lambda z . z * z) 4)

我们可以按不同的顺序来计算：我们可以首先对(lambda x y . x * y)做beta规约，于是有：

1
3 * ((lambda z . z * z) 4)

或者，我们可以先beta规约((lambda z . z * z) 4)：

1
(lambda x y . x * y) 3 (4 * 4)

在这种情况下，两种方式得到相同的结果；但事实并非总是如此。

第一种顺序就是我们所说的「惰性求值」（Lazy evaluation）：我们不计算函数的参数，直到我们需要使用它们。第二种叫「急切求值」（eager evaluation）：我们总是在把参数传递给函数之前进行计算。（在实际的编程语言中，Lisp语言，Scheme，和ML使用急切求值计算lambda演算，Haskell和Miranda则使用惰性值计算lambda演算。）我上面描述的Y组合子是惰性求值。如果我们用急切求值，那么上述Y组合子是导不出来的——事实上，它会永远地复制Y。

一点个人解释

Y在定义递归函数中的作用

首先，在lambda演算中，函数名不是不可缺少的，没有函数名的函数称为「匿名函数」。lambda符号的引入就是为了去掉函数名这个冗余，使定义匿名函数成为可能。但是当需要定义的函数含有递归时，比如阶乘factorial，也就是函数的定义部分需要引用函数自身的时候，没有函数名意味着用lambda演算无法直接引用函数自身。怎么办呢？

一种办法是设计另一个函数G，它接受一个函数作为参数，返回值也是一个函数（这种参数是函数的函数称为高阶函数）。然后，我们把factorial当做参数传给G，如果G返回的函数也是factorial的话，就圆满了。也就是说，这个G需要满足两个特征：

  1. G的定义中不会出现factorial，但是它可以接受factorial作为参数。回想一下一阶函数f(x) = x * x，它的定义里没有出现数字「1」，但是「1」可以传给它进行计算。而在构造G时，factorial就相当于数字「1」。
  2. 方程G(f)=f的解是factorial。这样我们就不用直接定义factorial，求解这个关于G的方程就可以得到factorial的定义了。

于是，我们需要干两件事：找到G，和找到求解G(f)=f的办法。寻找G很简单，既然我们想让G(factorial)=factorial，那么把factorial定义中关于factorial的引用参数化就可以了，即：

1
let G = lambda f . lambda n . IsZero n 1 (Mult n ( f (Pred n)))

这就是上面的metafact函数。这种构造方法可以用于构造任意递归函数的「G」。

然后我们需要找到求解方程G(f)=f的办法。满足f(x)=x的x称为函数f的不动点，f是高阶函数时也不例外。Y组合子的作用就是计算函数的不动点，它对所有的函数f都满足f(Y(f)) = Y(f)，推理如下：

1
2
3
4
5
6
Y (f) = (lambda y . (lambda x . y (x x)) (lambda x . y (x x))) f
    = (lambda x . f (x x)) (lambda x . f (x x)) 
    = (lambda x . f (x x)) (lambda a . f (a a))
    = f ((lambda a . f (a a)) (lambda a . f (a a)))
    = f ((lambda x . f (x x)) (lambda x . f (x x)))
    = f (Y(f))

于是，factorial的定义就可以写成：

1
2
3
factorial n = (Y metafact) n 
            = {[lambda y . (lambda t . y (t t)) (lambda t . y (t t))]
               [lambda f . lambda n . IsZero n 1 (Mult n ( f (Pred n)))]} n

这下不用引用自身了。

Y怎么来的

现在回到第一版的阶乘。我们虽然不能直接引用自身，但可以把它作为参数传进来，也就是说：

1
let fact2 = lambda f. lambda n . IsZero n 1 (Mult n ( f (Pred n)))

这样，在计算5的阶乘时，我们只需要计算fact2(fact2, 5)就可以了。定义并没有引用自身，只是在使用的时候把自己当参数传过去。是不是很简单？

但是，这个计算式是错误的：fact2的定义要求它接受两个参数，其中参数f是只接受一个参数的函数，于是计算式中第二个的fact2在参数数量上是无法和定义中的f匹配的。那怎么办？

不要紧，我们可以修改一下f的形式，让它接受两个参数。即：

1
let fact3 = lambda f. lambda n . IsZero n 1 (Mult n ( f [f, (Pred n)]))

这下计算fact3(fact3, 5)就不会出错了。除了这个定义有点丑……

如果对fact3做下化简又如何呢？首先是对拥有两个参数的f进行柯里化变换：

1
2
let fact3 = lambda h . lambda n . IsZero n 1 (Mult n ( h h (Pred n))) 
          = lambda h . lambda n . IsZero n 1 (Mult n ( (h h) (Pred n)))

这样计算阶乘的方式也相应变成了(fact3 fact3) 5。接着把(h h)用函数q代替，则有

1
2
let fact3 = lambda h . lambda n . [lambda q . IsZero n 1 (Mult n ( q (Pred n)))] (h h)
          = lambda h . [lambda n . lambda q . IsZero n 1 (Mult n ( q (Pred n)))] (h h)

仔细观察中括号部分，参数h对于这部分是完全自由的，于是我们可以用另一个函数定义替换之：

1
2
let f0 = lambda n . lambda q . IsZero n 1 (Mult n ( q (Pred n)))
let fact3 = lambda h . f0 (h h)

是不是觉得f0眼熟？没错，这就是metafact！不过我们先把f0放一边，看看如何使用这个定义计算n的阶乘。

1
2
factorail n = (fact3 fact3) n 
            = (lambda h . f0 (h h)) (lambda h . f0 (h h)) n

把上面的式子写成 function_name x的形式：

1
factorial n = {[lambda f . (lambda h . f (h h)) (lambda h . f (h h))] f0} n

注意大括号中的部分，是不是更眼熟了？这就是Y的定义。真是怎么绕都扰不过去的Y啊……

1
2
3
factorial n = {[lambda f . (lambda h . f (h h)) (lambda h . f (h h))] f0} n
            = {Y f0} n
            = (Y metafact) n